Duffing Oscillator
Description of the problem
Consider the nonlinear Duffing oscillator with governing dynamic equations given as
\begin{align} \begin{split} \dot{x}_1 &= x_2 + u_1\\ \dot{x}_2 &= -\beta x_1 - \delta x_2 - \alpha x_1^3 + u_2\\ \end{split} \end{align}
with $:nbsphinx-math:beta `= 4, $:nbsphinx-math:delta = 0.1 and :math:alpha = -1`. The training data set is comprised of two trajectories with initial conditions:
\begin{align} \begin{split} x_{0_1} &= \begin{bmatrix} 0.5 & 0.5 \end{bmatrix}^\top\\ x_{0_2} &= \begin{bmatrix} 1.4 & -0.2 \end{bmatrix}^\top. \end{split} \end{align}
with inputs:
\begin{align} \begin{split} u_{1}(t) &= 0\\ u_{2}(t) &= 0.3\cos(t) + \omega(t) \end{split} \end{align}
and \(\omega(t)\) sampled from a Gaussian distribution with zero mean and standard deviation \(\sigma = 0.1\).
The data are recorded at a frequency of \(50\)Hz for \(5\) seconds. An initial value of \(\lambda_1 = 10\) is chosen for the low-pass filter. The initial dictionary of basis functions consists of a total of 28 polynomial basis functions up to degree 5 in state variables.
Two cases are considered with the first test case corresponding to perfect measurements and the second test case corresponding to measurements being corrupted by zero mean Gaussian white noise of standard deviation \(10^{-4}\).
The code below shows how to use the python systemID package to find a sparse representation of the dynamics of the Duffing oscillator.
Case 1: No noise
First, import all necessary packages.
[1]:
import systemID as sysID
import numpy as np
import scipy.linalg as LA
import scipy.interpolate as interp
import matplotlib.pyplot as plt
from matplotlib import rc
plt.rcParams.update({"text.usetex": True, "font.family": "sans-serif", "font.serif": ["Computer Modern Roman"]})
rc('text', usetex=True)
plt.rcParams['text.latex.preamble'] = r"\usepackage{amsmath}"
Define the parameters of the study. Data is collected at a frequency of 50Hz.
[2]:
frequency = 50
total_time = 2
number_steps = int(total_time * frequency + 1)
tspan = np.linspace(0, total_time, number_steps)
Define the dynamics of the Duffing oscillator.
[3]:
state_dimension = 2
beta = 4
delta = 0.1
alpha = -1
def F(x, t, u):
dxdt = np.zeros(state_dimension)
dxdt[0] = x[1] + u(t)[0]
dxdt[1] = -beta * x[0] - delta * x[1] - alpha * x[0] ** 3 + u(t)[1]
return dxdt
def G(x, t, u):
return x
Generate the training data.
[4]:
number_experiments = 2
x0s = [np.array([0.5, 0.5]), np.array([1.4, -0.2])]
input_signals = []
output_signals = []
for i in range(number_experiments):
true_system = sysID.continuous_nonlinear_model(x0s[i], F, G=G)
input_signal_data = np.concatenate((np.zeros([1, number_steps]), 0.3 * np.cos(tspan) + 0.1 * np.random.randn(1, number_steps)), axis=0)
input_signal = sysID.continuous_signal(u=interp.interp1d(tspan, input_signal_data, kind='cubic', bounds_error=False, fill_value=input_signal_data[:, -1]))
input_signals.append(sysID.discrete_signal(frequency=frequency, data=input_signal_data))
output_signals.append(sysID.propagate(input_signal, true_system, tspan=tspan)[0])
Plot training trajectories.
[5]:
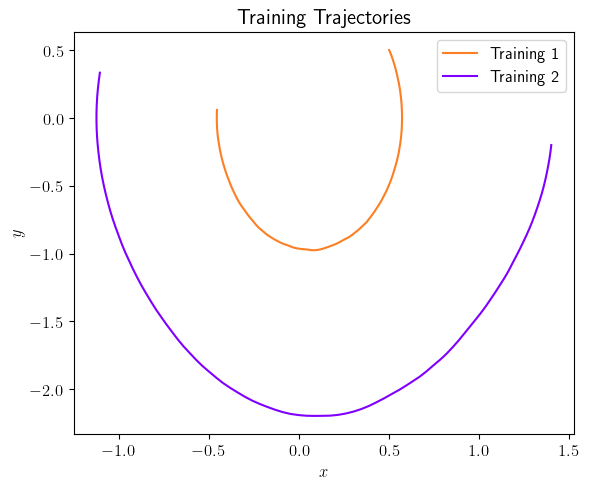
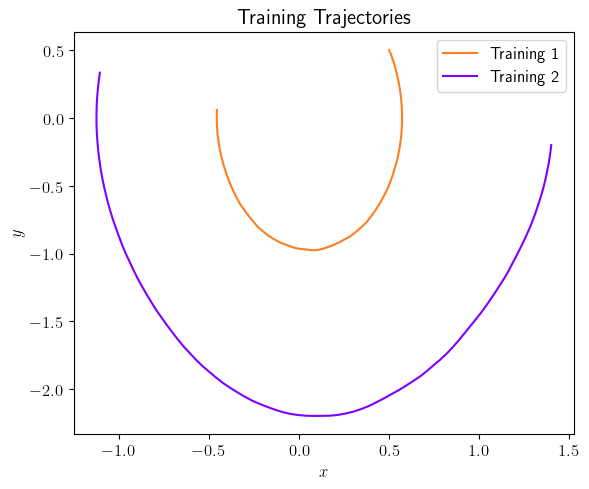
fig = plt.figure(num=2, figsize=[6, 5])
ax = fig.add_subplot(1, 1, 1)
ax.plot(output_signals[0].data[0, :], output_signals[0].data[1, :], color=(253/255, 127/255, 35/255), label='Training 1')
ax.plot(output_signals[1].data[0, :], output_signals[1].data[1, :], color=(127/255, 0/255, 255/255), label='Training 2')
ax.set_xlabel(r'$x$', fontsize=12)
ax.set_ylabel(r'$y$', fontsize=12)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.title(r'Training Trajectories', fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
Generate list of polynomial basis functions up to order 6.
[6]:
order = 6
index = sysID.polynomial_index(state_dimension, order, max_order=order)
basis_functions = sysID.polynomial_basis_functions(index)
Solve least-squares and \(\ell-1\) norm minimization problem.
[7]:
filter_coefficient = 10
relax_coefficient = 2
threshold = 1e-2
max_iterations = 5
init_weight = 'least_squares'
sparse = sysID.sparse_1st_order(input_signals, output_signals, basis_functions, filter_coefficient, relax_coefficient, threshold, max_iterations, init_weight=init_weight)
Dimension 1 of 2
Signal number 1 of 2
Signal number 2 of 2
Iteration: 0
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
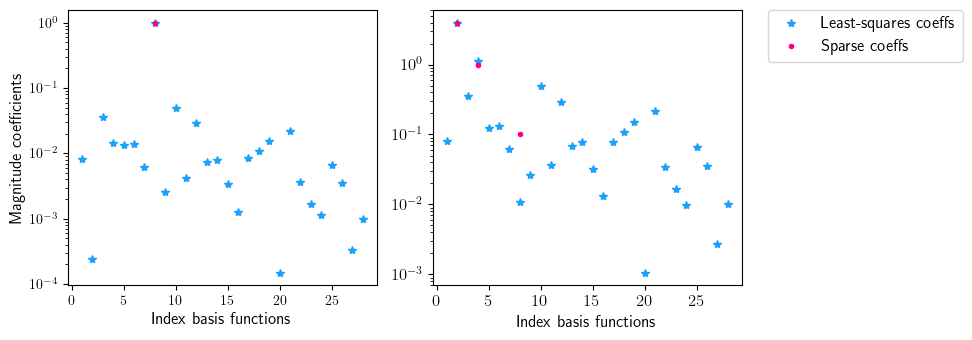
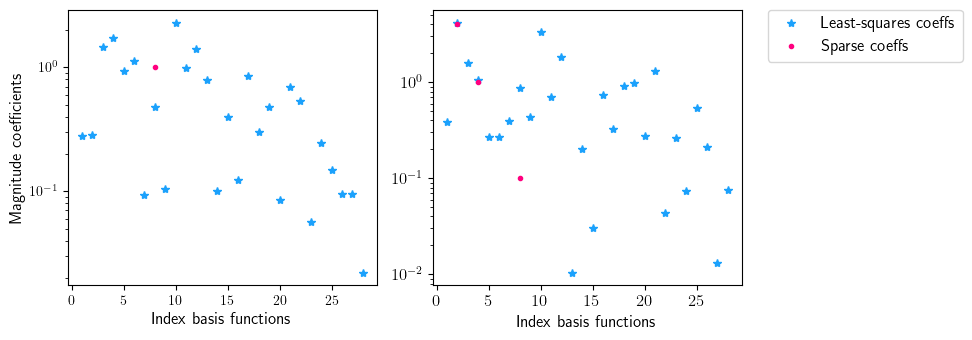
indices non zero: [7]
indices zero: [0, 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27]
Dimension 2 of 2
Signal number 1 of 2
Signal number 2 of 2
Iteration: 0
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
indices non zero: [1, 3, 7]
indices zero: [0, 2, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27]
Represent coefficients.
[8]:
fig = plt.figure(num=2, figsize=[10, 3.5])
ax = fig.add_subplot(1, 2, 1)
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_least_squares[:, 0]), '*', color=(27/255, 161/255, 252/255), label='Least-squares coeffs')
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_sparse[:, 0]), '.', color=(255/255, 0/255, 127/255), label='Sparse coeffs')
ax.set_xlabel(r'Index basis functions', fontsize=12)
ax.set_ylabel(r'Magnitude coefficients', fontsize=12)
ax = fig.add_subplot(1, 2, 2)
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_least_squares[:, 1]), '*', color=(27/255, 161/255, 252/255), label='Least-squares coeffs')
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_sparse[:, 1]), '.', color=(255/255, 0/255, 127/255), label='Sparse coeffs')
ax.set_xlabel(r'Index basis functions', fontsize=12)
ax.legend(loc='upper center', bbox_to_anchor=(1.4, 1.03), ncol=1, fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
The two sets of coefficients are now used on an unseen trajectory for 10 seconds.
[9]:
total_time_testing = 10
number_steps_testing = int(total_time_testing * frequency + 1)
tspan_testing = np.linspace(0, total_time_testing, number_steps_testing)
x0_test = np.array([-0.3, 0.2])
true_system_test = sysID.continuous_nonlinear_model(x0_test, F, G=G)
def u_test(t):
return np.array([0 * t, 0.4 * np.exp(-t) * np.sin(0.1 * t)])
input_signal_test = sysID.continuous_signal(u=u_test)
output_signal_test = sysID.propagate(input_signal_test, true_system_test, tspan=tspan_testing)[0]
def F_least_squares(x, t, u):
dxdt = np.zeros([state_dimension])
for i in range(len(basis_functions)):
dxdt = dxdt + np.transpose(basis_functions[i](x) * sparse.coefficients_least_squares[i, :])
dxdt = dxdt + u(t)
return dxdt
def F_sparse(x, t, u):
dxdt = np.zeros([state_dimension])
for i in range(len(basis_functions)):
dxdt = dxdt + np.transpose(basis_functions[i](x) * sparse.coefficients_sparse[i, :])
dxdt = dxdt + u(t)
return dxdt
least_squares_system_test = sysID.continuous_nonlinear_model(x0_test, F_least_squares, G=G)
sparse_system_test = sysID.continuous_nonlinear_model(x0_test, F_sparse, G=G)
least_squares_output_signal_test = sysID.propagate(input_signal_test, least_squares_system_test, tspan=tspan_testing)[0]
sparse_output_signal_test = sysID.propagate(input_signal_test, sparse_system_test, tspan=tspan_testing)[0]
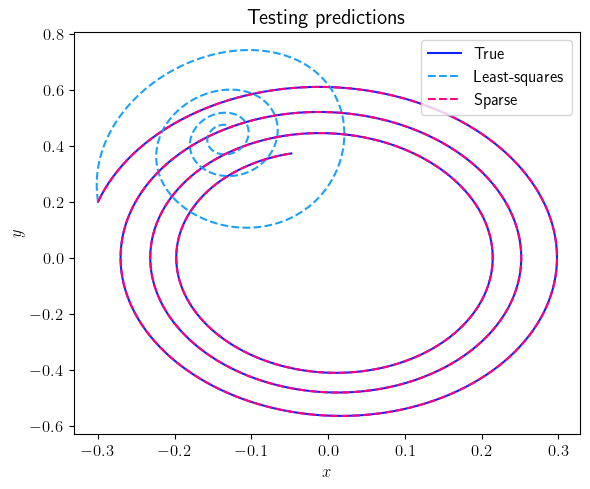
fig = plt.figure(num=3, figsize=[6, 5])
ax = fig.add_subplot(1, 1, 1)
ax.plot(output_signal_test.data[0, :], output_signal_test.data[1, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(least_squares_output_signal_test.data[0, :], least_squares_output_signal_test.data[1, :], '--', color=(27/255, 161/255, 252/255), label=r'Least-squares')
ax.plot(sparse_output_signal_test.data[0, :], sparse_output_signal_test.data[1, :], '--', color=(255/255, 0/255, 127/255), label=r'Sparse')
ax.set_xlabel(r'$x$', fontsize=12)
ax.set_ylabel(r'$y$', fontsize=12)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.title(r'Testing predictions', fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
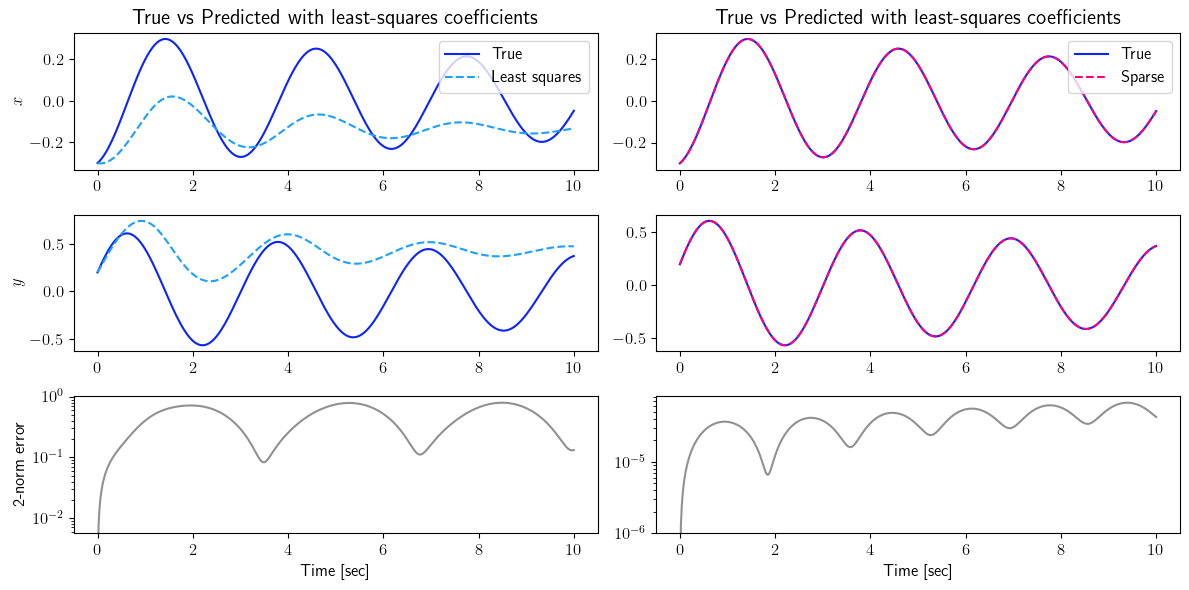
fig = plt.figure(num=4, figsize=[12, 6])
ax = fig.add_subplot(3, 2, 1)
ax.plot(tspan_testing, output_signal_test.data[0, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, least_squares_output_signal_test.data[0, :], '--', color=(27/255, 161/255, 252/255), label=r'Least squares')
plt.ylabel(r'$x$', fontsize=12)
plt.title(r'True vs Predicted with least-squares coefficients', fontsize=15)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 2)
ax.plot(tspan_testing, output_signal_test.data[0, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, sparse_output_signal_test.data[0, :], '--', color=(255/255, 0/255, 127/255), label=r'Sparse')
plt.title(r'True vs Predicted with least-squares coefficients', fontsize=15)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 3)
ax.plot(tspan_testing, output_signal_test.data[1, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, least_squares_output_signal_test.data[1, :], '--', color=(27/255, 161/255, 252/255), label=r'Least squares')
plt.ylabel(r'$y$', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 4)
ax.plot(tspan_testing, output_signal_test.data[1, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, sparse_output_signal_test.data[1, :], '--', color=(255/255, 0/255, 127/255), label=r'Sparse')
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 5)
ax.semilogy(tspan_testing, LA.norm(output_signal_test.data - least_squares_output_signal_test.data, axis=0), color=(145/255, 145/255, 145/255))
plt.ylabel(r'2-norm error', fontsize=12)
plt.xlabel(r'Time [sec]', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 6)
ax.semilogy(tspan_testing, LA.norm(output_signal_test.data - sparse_output_signal_test.data, axis=0), color=(145/255, 145/255, 145/255))
plt.xlabel(r'Time [sec]', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
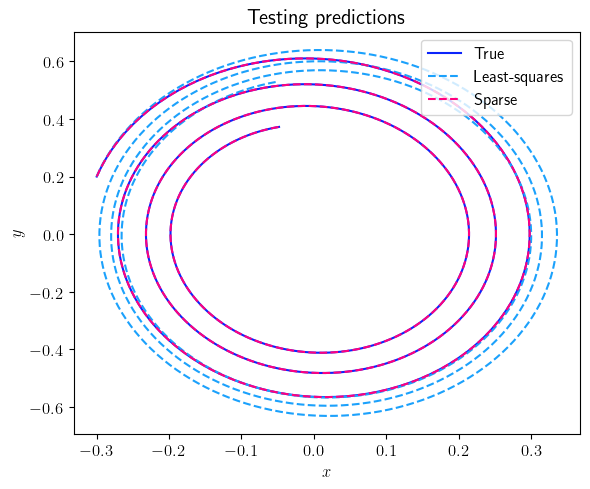
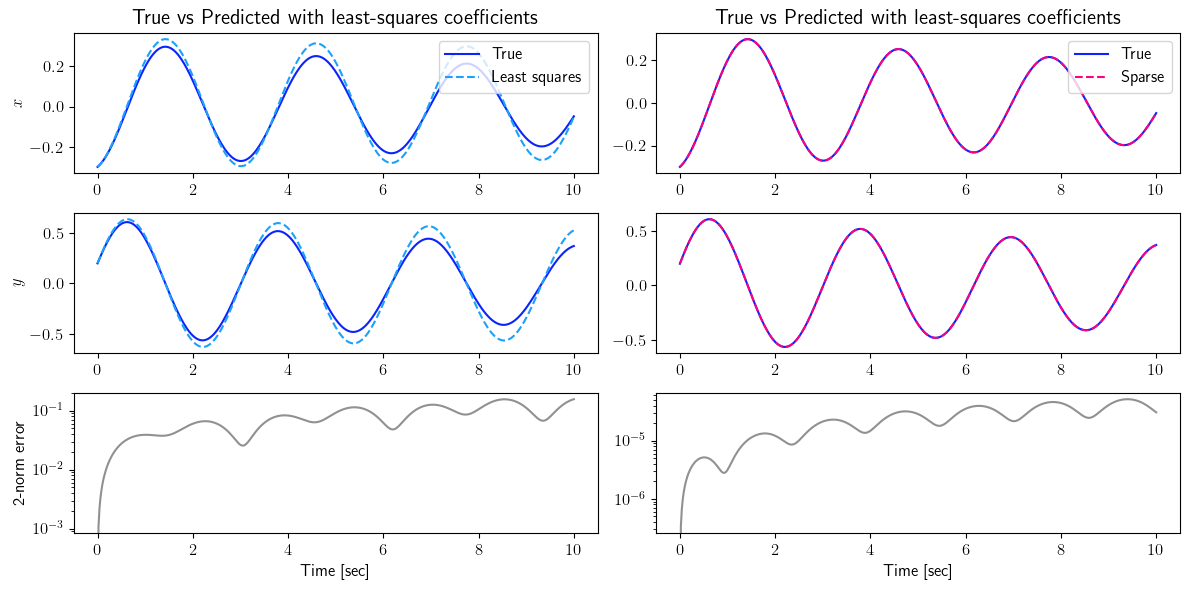
Case 2: Measurements with additive white noise
Now, a Gaussian noise with standard deviation \(10^{-4}\) is added to the measured output signal. The filter coefficient is set to 1, the threshold is lifted right above the noise level to 0.1 and the relaxation coefficient is tightened to 1.5.
[10]:
for i in range(number_experiments):
output_signals[i].data = output_signals[i].data + 1e-4 * np.random.randn(state_dimension, number_steps)
fig = plt.figure(num=2, figsize=[6, 5])
ax = fig.add_subplot(1, 1, 1)
ax.plot(output_signals[0].data[0, :], output_signals[0].data[1, :], color=(253/255, 127/255, 35/255), label='Training 1')
ax.plot(output_signals[1].data[0, :], output_signals[1].data[1, :], color=(127/255, 0/255, 255/255), label='Training 2')
ax.set_xlabel(r'$x$', fontsize=12)
ax.set_ylabel(r'$y$', fontsize=12)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.title(r'Training Trajectories', fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
[11]:
order = 6
index = sysID.polynomial_index(state_dimension, order, max_order=order)
basis_functions = sysID.polynomial_basis_functions(index)
filter_coefficient = 1
relax_coefficient = 1.5
threshold = 1e-1
max_iterations = 5
init_weight = 'least_squares'
sparse = sysID.sparse_1st_order(input_signals, output_signals, basis_functions, filter_coefficient, relax_coefficient, threshold, max_iterations, init_weight=init_weight)
fig = plt.figure(num=2, figsize=[10, 3.5])
ax = fig.add_subplot(1, 2, 1)
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_least_squares[:, 0]), '*', color=(27/255, 161/255, 252/255), label='Least-squares coeffs')
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_sparse[:, 0]), '.', color=(255/255, 0/255, 127/255), label='Sparse coeffs')
ax.set_xlabel(r'Index basis functions', fontsize=12)
ax.set_ylabel(r'Magnitude coefficients', fontsize=12)
ax = fig.add_subplot(1, 2, 2)
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_least_squares[:, 1]), '*', color=(27/255, 161/255, 252/255), label='Least-squares coeffs')
ax.semilogy(np.linspace(1, len(index), len(index)), np.abs(sparse.coefficients_sparse[:, 1]), '.', color=(255/255, 0/255, 127/255), label='Sparse coeffs')
ax.set_xlabel(r'Index basis functions', fontsize=12)
ax.legend(loc='upper center', bbox_to_anchor=(1.4, 1.03), ncol=1, fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
Dimension 1 of 2
Signal number 1 of 2
Signal number 2 of 2
Iteration: 0
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
indices non zero: [7]
indices zero: [0, 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27]
Dimension 2 of 2
Signal number 1 of 2
Signal number 2 of 2
Iteration: 0
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
indices non zero: [1, 3, 7]
indices zero: [0, 2, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27]
[12]:
total_time_testing = 10
number_steps_testing = int(total_time_testing * frequency + 1)
tspan_testing = np.linspace(0, total_time_testing, number_steps_testing)
x0_test = np.array([-0.3, 0.2])
true_system_test = sysID.continuous_nonlinear_model(x0_test, F, G=G)
def u_test(t):
return np.array([0 * t, 0.4 * np.exp(-t) * np.sin(0.1 * t)])
input_signal_test = sysID.continuous_signal(u=u_test)
output_signal_test = sysID.propagate(input_signal_test, true_system_test, tspan=tspan_testing)[0]
def F_least_squares(x, t, u):
dxdt = np.zeros([state_dimension])
for i in range(len(basis_functions)):
dxdt = dxdt + np.transpose(basis_functions[i](x) * sparse.coefficients_least_squares[i, :])
dxdt = dxdt + u(t)
return dxdt
def F_sparse(x, t, u):
dxdt = np.zeros([state_dimension])
for i in range(len(basis_functions)):
dxdt = dxdt + np.transpose(basis_functions[i](x) * sparse.coefficients_sparse[i, :])
dxdt = dxdt + u(t)
return dxdt
least_squares_system_test = sysID.continuous_nonlinear_model(x0_test, F_least_squares, G=G)
sparse_system_test = sysID.continuous_nonlinear_model(x0_test, F_sparse, G=G)
least_squares_output_signal_test = sysID.propagate(input_signal_test, least_squares_system_test, tspan=tspan_testing)[0]
sparse_output_signal_test = sysID.propagate(input_signal_test, sparse_system_test, tspan=tspan_testing)[0]
fig = plt.figure(num=3, figsize=[6, 5])
ax = fig.add_subplot(1, 1, 1)
ax.plot(output_signal_test.data[0, :], output_signal_test.data[1, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(least_squares_output_signal_test.data[0, :], least_squares_output_signal_test.data[1, :], '--', color=(27/255, 161/255, 252/255), label=r'Least-squares')
ax.plot(sparse_output_signal_test.data[0, :], sparse_output_signal_test.data[1, :], '--', color=(255/255, 0/255, 127/255), label=r'Sparse')
ax.set_xlabel(r'$x$', fontsize=12)
ax.set_ylabel(r'$y$', fontsize=12)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.title(r'Testing predictions', fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
fig = plt.figure(num=4, figsize=[12, 6])
ax = fig.add_subplot(3, 2, 1)
ax.plot(tspan_testing, output_signal_test.data[0, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, least_squares_output_signal_test.data[0, :], '--', color=(27/255, 161/255, 252/255), label=r'Least squares')
plt.ylabel(r'$x$', fontsize=12)
plt.title(r'True vs Predicted with least-squares coefficients', fontsize=15)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 2)
ax.plot(tspan_testing, output_signal_test.data[0, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, sparse_output_signal_test.data[0, :], '--', color=(255/255, 0/255, 127/255), label=r'Sparse')
plt.title(r'True vs Predicted with least-squares coefficients', fontsize=15)
ax.legend(loc='upper right', ncol=1, fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 3)
ax.plot(tspan_testing, output_signal_test.data[1, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, least_squares_output_signal_test.data[1, :], '--', color=(27/255, 161/255, 252/255), label=r'Least squares')
plt.ylabel(r'$y$', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 4)
ax.plot(tspan_testing, output_signal_test.data[1, :], color=(11/255, 36/255, 251/255), label=r'True')
ax.plot(tspan_testing, sparse_output_signal_test.data[1, :], '--', color=(255/255, 0/255, 127/255), label=r'Sparse')
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 5)
ax.semilogy(tspan_testing, LA.norm(output_signal_test.data - least_squares_output_signal_test.data, axis=0), color=(145/255, 145/255, 145/255))
plt.ylabel(r'2-norm error', fontsize=12)
plt.xlabel(r'Time [sec]', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax = fig.add_subplot(3, 2, 6)
ax.semilogy(tspan_testing, LA.norm(output_signal_test.data - sparse_output_signal_test.data, axis=0), color=(145/255, 145/255, 145/255))
plt.xlabel(r'Time [sec]', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.show()
